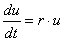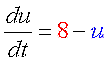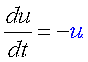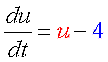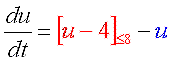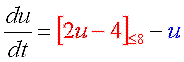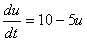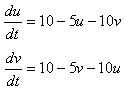フィードバック、遺伝子スイッチ(双安定系)
文責:尾崎 淳
生物=フィードバック回路の集合体
以前の解説ページの序文にも書いたが、私は“何をしたいのか”・“どう表現したいのか”にこだわります。
それをハッキリさせるためには、怒涛の勢いで量産される論文を追いかけるだけではダメで、少し引いた目で興味の対象を眺める視点が大事になります。
ふたたび繰り返しちゃいますが、“生物らしさ”ってなんでしょうね?
生物といえども物質からできています。 でも明らかに私たちは「生物」を、通常言うところの「物質」とは分けています。
「もの」なのに「もの」らしくない=“生物らしさ”。
“生物らしさ”が生まれる瞬間、それを明らかにしたい・・これが、私が生物学を始めた原点です。
結論から言ってしまうと、フィードバックこそが“生物らしさ”を生む物質的基盤である、と考えています(他にも、分子認識の特異性とかもあるけど)。 これがあるから、ニョキニョキ成長したりドクドク拍動したり、という(私が考える)“生物らしさ”が生まれるのです。 考えてみたら当然ですよね?
分子や細胞のいる世界はノイズだらけの世界です。
意思などもっていない分子や細胞が整然と振る舞うには、シグナルがノイズの海にかき消されないメカニズムが必要です。
それを可能にするのはフィードバックです。
また、一方向的な矢印でメカニズムを考えている論文や発表をよく見ますが、それだけでは系は安定に存在しないですよね?
合成のみor抑制のみでは死んじゃいます。
目の前の実験対象が安定に存在している・・ただそれだけでも、中にはフィードバックが働いている、と考えるべきなのです。
|
| ||||||||||||
 |
負のフィードバックの利点は明らかでしょう。 生化学の教科書にもよく載っているように、ホメオスタシス(恒常性)として機能しています。
また濃度のゆらぎ(ノイズ)を緩和させる働きもあります。
負のフィードバックがあるから、生物は死なずに安定に維持できるのです。
一方で、正のフィードバックは、それほど教科書では大きく扱われていないように感じられます。
せいぜいホルモン等の、微量シグナルの増幅機構として紹介しているぐらいでしょうか?
正のフィードバックは、それだけでは系を不安定化するので、“調節”という観点からはあまりイメージが良くないのでしょうか、負のフィードバックほどには重要視されていないようです。
しかし、これから以下に示すように、“生き生きとした”振る舞いを生み出す源は正のフィードバックの方なのです。
正のフィードバックがあるからニョキニョキ成長したりドクドク拍動したりするのです。
よく論文で、興味の対象がニョキニョキ・ドクドクの解明なハズなのに(生物学の興味はほとんどそれでしょ)、モデルに正のフィードバックが入っていないものが見られます(これまた、ほとんどがそう)。 私から見れば、それだけで「だみだこりゃ」と感じてしまいます。
だって一番の核心部が抜けているんですからね。
遺伝子スイッチ(=双安定系)
フィードバックから双安定系をつくる
ニョキニョキ(パターン形成)やドクドク(振動・興奮)をつくる前に、まずスイッチ(ON/OFF2状態をもつ系)をつくります。 2つの安定な状態をもつので、この様な反応系を“双安定(bistable)系”といいます。 双安定系をもとにパターン形成や振動などは生まれるのです。 しかしながら、双安定系は決して単なる次の段階への準備ではありません。 これだけでも多くの生命現象の解釈には有用なのです。 それは細胞の分化です。 細胞の分化とは、同じゲノムを持った細胞が異なる分子組成で安定に維持されている状態、ということでしょう。 では、その様なことを可能にするには、シグナル・ネットワークにどの様な関係があればよいのでしょうか?
|
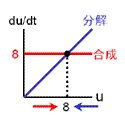
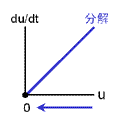
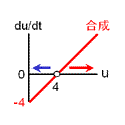
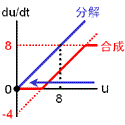
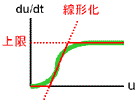
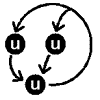
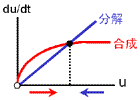
もっともシンプルに、2つの安定状態をもつ反応ネットワークをつくることを考える。 安定化の源は負のフィードバックでしたね。 そこで、右の2つのフィードバック回路がからむ、と考えます。 最終的に収束する濃度は合成と分解のバランスで決まります(真ん中の列)。 合成が勝っている領域では増大方向、分解が勝っている領域では減少方向に動きます。 しかし、この2つの反応系を足し合わせても双安定系にはなりません。 第3の収束値をもつ単安定系になるだけです。 |
| |||||||||
 |
|
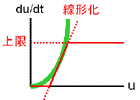
双安定にするには、2つの安定状態の間に不安定状態を入れる必要があります。
そこで登場するのが正のフィードバックです。 |
| |||
 |
さあ、これら3式を足し合わせたら双安定系はできるでしょうか?
残念ながら、単純に足すだけではできません。
少し工夫します。
|
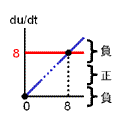
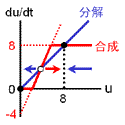
収束値(いまの場合8と0)を決めるのは負のフィードバック回路の合成項です。 ですから、ここが変わってしまうと収束値も動いてしまいます。 そこで合成の上限・下限は負のフィードバックの式で固定しちゃいます。 また、正のフィードバックの“分解”項(-4)は、単に分岐点の位置調整の意味しかないので、“合成”項に含めちゃいます。 要は右図のように“負のフィードバックっぽい振る舞い”をするところと“正のフィードバックっぽい振る舞い”をするところとに分けるのです。 |
| |
 |
|
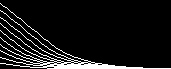
結果が右です。 ダメですね・・ |
| |||
 |
理由は合成・分解のバランス図を見れば明らかですよね? 常に分解の方が勝っているからです。 どうすればよいでしょう?
簡単です。
正のフィードバックの係数を大きくしてあげればよいのです。 この程度の微調整は、何ら話しの本筋を損ねません。
|
双安定系、完成です! |
| |||
 |
2つの安定状態(←負のフィードバックによる)を分ける正のフィードバックが大事な役割をしていることが分かるでしょう。
式の形なんて、本質ではないのだよ
上の話では、最後の操作が作為的で、何か気持ち悪いと感じた人がいるかもしれない。 しかし以下を読めば、むしろこの方がイメージが湧きやすいことがわかるだろう。
|
より現実的な生化学反応を考えると、一般に反応速度はHillの式
|
| |||
 |
「反応速度に上限がある」というのは「分子の数が有限である」ということの反映です。 よって上の操作で合成速度に上限を設けたのは、現実に照らして何ら問題ない仮定であることが分かるでしょう。
|
しかし合成の項の“-4”の部分には生化学的な意味は全くないから、もう少し修正を加えてもよさそうです。 |
| ||
 |
|
ちなみにHillの式でn=1とおくと、おなじみのMichaelis-Mentenの式になります(右図赤線)。 この式では双安定性は生まれません。 当然それは、Michaelis-Mentenのモデルには協同作用が入っていないことを意味します。 |
| |
 |
まとめると「合成速度un + 上限 =
Hillの式」ということです。
実際、“道具”として反応拡散系を使うときには、このように意味のある部品ごとに分けた方が「一体何が起こっているのか」を把握しやすい。
小ぎれいにHillの式なんかにまとめちゃうと、パラメータを変えたときに、どこに作用したのか、が分かりにくくなる。
いや、むしろ逆にHillの式を上記のように分割して「この辺は“負のフィードバックっぽい振る舞い”をするところだな」と見たときに初めてHillの式の意味が解かるってもんでしょ。
チューリングは線形の式を使って反応拡散系のエッセンスを描きました。
しかし彼は細かいところを省略したので、そのままをシミュレーションすると結果は奇妙な振る舞いをしてしまいます。
それをもって線形の式を批判する人がいますが、全くトンチンカンな批判です。 線形モデル以上にイメージが湧きやすいモデルはありません!
当サイトのシミュレータは線形近似の式を採用しています。 反応拡散系の特徴的なダイナミクスは、これでほとんど表現可能です。
負のフィードバック×負のフィードバック=正のフィードバック
これまで、双安定系を生むための最低限の要素として、2つの負のフィードバックと1つの正のフィードバックが必要だと言ってきました。
しかし現実的なことを考えると「そんなに都合のいい系はあるのか?」と感じている人もいることでしょう。
その点についてコメントしておきます。
“負のフィードバック”と言ってきましたが、これは必ずしも積極的な“抑制”である必要はありません。
式の形を見れば分かるように、この効果は単なる分子の分解で代用できます。 実際には、ほとんどがこのケースでしょう。
ですから、2つの負のフィードバックの効果(上限と下限)は、“有限の分子数”と“分子の分解”という、ごく当たり前の事象で機能できるのです。
それでは正のフィードバックの方はどうでしょうか?
いままでは1変数で記述してきたので積極的な“自己触媒”をイメージする書き方をしてきました。 しかし2変数以上の系を考えれば(実際にはこちらでしょう)、必ずしも直接の自己触媒である必要はないのです。
|
例えば
実はこれだけで双安定系はできてしまうのです。 |
| |||||
 |
これは互いの抑制が、それぞれにとって正味“正のフィードバック”の効果を生んでいるからです。
つまり、uが少し増える→(uからの抑制が強まり)vが少し減る→(vからの抑制が弱まり)uがさらに増える・・で雪ダルマ式に差が増大していくのです(=正のフィードバック)。
右上のシミュレーションでは、vの初期値を“1”(緑線)にしたとき、いろいろなuの値がどこに収束するかを示したものです。
1よりも大きい値を出発すると“2”へ(このときvは“0”へ)、小さい値を出発すると“0”へ(このときvは“2”へ)収束します。
この様な反応系の存在はすでに生物で確かめられています。
有名なλファージの溶原化のメカニズムです。λリプレッサーとCroタンパク質が相互抑制しあい双安定系(遺伝子スイッチ)を作っているのです。